Automata to Pyramids - Hi friends, I hope you are all in good healthEDUCATION, In the article you are reading this time with the title Automata to Pyramids, We have prepared this article well for you to read and take information in it. hopefully the contents of the post what we write you can understand. ok, happy reading.

Title : Automata to Pyramids
link : Automata to Pyramids

Automata to Pyramids

Was flipping through Steven Wolfram's A New Kind of Science and was struck by the picture of the steps in the evolution of this 2D cellular automaton:

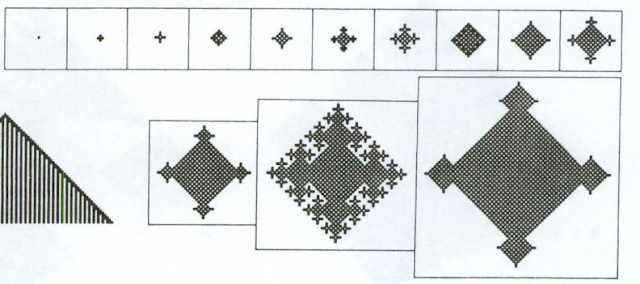
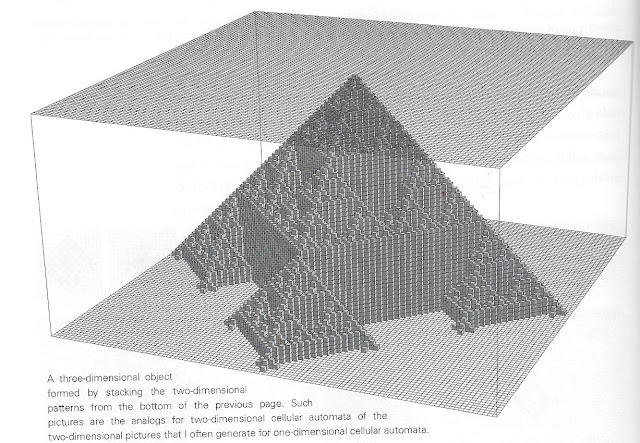
If every step became a level in a 3D shape, it'd look like this:



I'm motivated to try this out in Python. The first challenge is to create an array. It's easy enough to type in an 11x11 array for step 0 manually:

     surface = [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]

But we eventually want a bigger array. It should be easy to create, right? Here's the code for it:

tableSize = 11
surface = tableSize*[tableSize*[0]]

Which gives us a 11x11 array of all zeroes.



The code for making the middle one a 1 is this:

surface[int(tableSize/2)][int(tableSize/2)] = 1

Strangely, that produces this!

Numpy to the Rescue

I have no idea why this glitch is happening, so let's switch to Numpy, Python's professional-strength array-wrangling package. The code for making the array is easier, and it works:

    tableSize = 101
    surface = numpy.zeros((tableSize,tableSize))
    surface[int(tableSize/2)][int(tableSize/2)] = 1



Now I can make a monster array just by changing the tableSize variable.

Automating the Pattern

Now the question is how to produce the pattern in the first picture. For each cell, the program has to check its four neighbors (left, right, up, down) and see whether exactly 1 or 4 of the neighbors is a 1. If so (or if the cell itself is a 1), the cell is a 1 in the next level. This function will count the number of 1's among a cell's four neighbors:

def nbs(listA,r,c):
    '''counts the 1's in the 4 neighbors of a cell'''
    neighborList = []
    neighborList.append(listA[r-1][c])
    neighborList.append(listA[r][c-1])
    neighborList.append(listA[r][c+1])
    neighborList.append(listA[r+1][c])
    #count the 1's in the list
    return neighborList.count(1)

The function for the level needs to go through every row and column, check the neighbor number of the cell, and create the next level's cell. I called it "wolfram" after the author who inspired the exploration. The "enumerate" function is getting a workout.

def wolfram(level):
    '''returns the array for level'''
    #make the level 0 array
    tableSize = 11
    surface = numpy.zeros((tableSize,tableSize))
    surface[int(tableSize/2)][int(tableSize/2)] = 1
    
    for i in range(level): #repeat for each level
        newSurface = []     #empty list for next level
        for r,u in enumerate(surface): # for each row in array
            newSurface.append([]) #empty list in next level
            for c,v in enumerate(u): # for every item in row
                #if it has exactly 1 or 4 neighbors that are 1's
                if nbs(surface,r,c) in [1,4] or v == 1:
                    newSurface[r].append(1) #put a 1 in next level
                else: #otherwise
                    newSurface[r].append(0) #put a 0 in next level
        #replace the old level with new one for next loop
        surface = newSurface 
    return numpy.array(surface)

Unfortunately, this gives me an error when checking the cells on the sides of the array.

IndexError: index 11 is out of bounds for axis 0 with size 11

The "nbs" function has to be adjusted so it won't panic if there isn't a previous row or next column. The exception keyword in Python comes in handy again. Now I can tell it to "try" searching the neighbors and if it gets a urge to throw an IndexError at me, just move on.

def nbs(listA,r,c):
    '''puts 4 neighbors of a cell into a list'''
    neighborList = []
    try:
        neighborList.append(listA[r-1][c])
        neighborList.append(listA[r][c-1])
        neighborList.append(listA[r][c+1])
        neighborList.append(listA[r+1][c])
        
    except IndexError:
        pass
    return neighborList.count(1)

Now printing "wolfram(3)" gives me an array representing the 4th step in the first picture:

On to Higher Dimensions

So now I can generate an array for any level I want. Time to make a huge array and place blocks for each 1 in that level. I take my file and add the code necessary to make and display a 3D model in Pi3D, my favorite 3D graphics package. Here's the relevant code for taking the levels and making them layers of the pyramid:

cubeList = [] #list for storing cubes

#loop over each level:

for i in range(50,-1,-1): #50 levels, going down to 0

    rowList = wolfram(i)  #get the array for that "layer"

    for row,value in enumerate(rowList): #loop through the rows

for j,v in enumerate(value): #loop through the columns

   if v == 1: #if the value of that cell is 1

                #put a cube there

cubeList.append(pi3d.Cuboid(x=row,

                                            y=-i,

                                            z=j))

Then it's just a matter of iterating over the cube list and drawing all the cubes. Here's the final outcome in pi3d:

Finally I fire up the Raspberry Pi version of Minecraft and use the "setBlock" function to create the pyramid in a 3D world!

That's the article Automata to Pyramids

That's it for the article Automata to Pyramids this time, hopefully can be useful for all of you. okay, see you in another article post.

You are now reading the article Automata to Pyramids with link address https://educationviralnew.blogspot.com/2016/04/automata-to-pyramids.html